GLAD
crowdkit.aggregation.classification.glad.GLAD | Source code
GLAD( self, n_iter: int = 100, tol: float = 1e-05, silent: bool = True, labels_priors: Optional[Series] = None, alphas_priors_mean: Optional[Series] = None, betas_priors_mean: Optional[Series] = None, m_step_max_iter: int = 25, m_step_tol: float = 0.01)The GLAD (Generative model of Labels, Abilities, and Difficulties) model is a probabilistic model that parametrizes the abilities of workers and the difficulty of tasks.
Let's consider a case of class classification. Let be a vector of prior class probabilities, be a worker ability parameter, be an inverse task difficulty, be a latent variable representing the true task label, and be a worker response that we observe. The relationships between these variables and parameters according to GLAD are represented by the following latent label model:
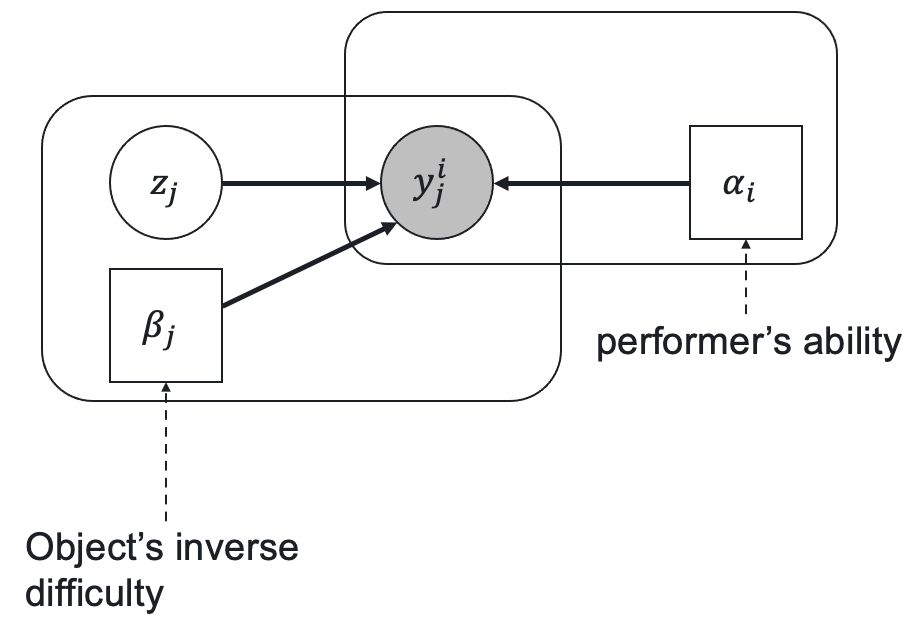
The prior probability of being equal to is
,
and the probability distribution of the worker responses with the true label follows the single coin Dawid-Skene model where the true label probability is a sigmoid function of the product of the worker ability and the inverse task difficulty:
,
where
.
Parameters , , , and latent variables are optimized with the Expectation-Minimization algorithm:
- E-step. Estimates the true task label probabilities using the alpha parameters of workers' abilities, the prior label probabilities, and the beta parameters of task difficulty.
- M-step. Optimizes the alpha and beta parameters using the conjugate gradient method.
J. Whitehill, P. Ruvolo, T. Wu, J. Bergsma, and J. Movellan. Whose Vote Should Count More: Optimal Integration of Labels from Labelers of Unknown Expertise.
Proceedings of the 22nd International Conference on Neural Information Processing Systems, 2009
https://proceedings.neurips.cc/paper/2009/file/f899139df5e1059396431415e770c6dd-Paper.pdf
Parameters description
| Parameters | Type | Description |
|---|---|---|
n_iter | int | The maximum number of EM iterations. |
tol | float | The tolerance stopping criterion for iterative methods with a variable number of steps. The algorithm converges when the loss change is less than the |
silent | bool | Specifies if the progress bar will be shown (false) or not (true). |
labels_priors | Optional[Series] | The prior label probabilities. |
alphas_priors_mean | Optional[Series] | The prior mean value of the alpha parameters. |
betas_priors_mean | Optional[Series] | The prior mean value of the beta parameters. |
m_step_max_iter | int | The maximum number of iterations of the conjugate gradient method in the M-step. |
m_step_tol | float | The tolerance stopping criterion of the conjugate gradient method in the M-step. |
labels_ | Optional[Series] | The task labels. The |
probas_ | Optional[DataFrame] | The probability distributions of task labels. The |
alphas_ | Series | The alpha parameters of workers' abilities. The |
betas_ | Series | The beta parameters of task difficulty. The |
loss_history_ | List[float] | A list of loss values during training. |
Examples:
from crowdkit.aggregation import GLADfrom crowdkit.datasets import load_datasetdf, gt = load_dataset('relevance-2')glad = GLAD()result = glad.fit_predict(df)Methods summary
| Method | Description |
|---|---|
| fit | Fits the model to the training data with the EM algorithm. |
| fit_predict | Fits the model to the training data and returns the aggregated results. |
| fit_predict_proba | Fits the model to the training data and returns probability distributions of labels for each task. |
Last updated: March 31, 2023